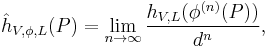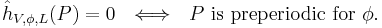Néron–Tate height
In number theory, the Néron–Tate height (or canonical height) is a quadratic form on the Mordell-Weil group of rational points of an abelian variety defined over a global field. It is named after André Néron and John Tate.
Contents |
Definition and properties
Néron defined the Néron–Tate height as a sum of local heights.[1] Tate (unpublished) defined it globally by observing that the logarithmic height hL associated to an invertible sheaf L on an abelian variety A is “almost quadratic,” and used this to show that the limit
exists and defines a quadratic form on the Mordell-Weil group of rational points.
The Néron–Tate height depends on the choice of an invertible sheaf (or an element of the Néron-Severi group) on the abelian variety. If the abelian variety A is defined over a number field K and the invertible sheaf is ample, then the Néron–Tate height is positive definite in the sense that it vanishes only on torsion elements of the Mordell-Weil group A(K). More generally, 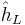 induces a positive definite quadratic form on the real vector space
induces a positive definite quadratic form on the real vector space 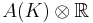 .
.
On an elliptic curve, the Néron-Severi group is of rank one and has a unique ample generator, so this generator is often used to define the Néron–Tate height, which is denoted 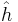 without reference to a particular line bundle. (However, the height that naturally appears in the statement of the Birch–Swinnerton-Dyer conjecture is twice this height.) On abelian varieties of higher dimension, there need not be a particular choice of smallest ample line bundle to be used in defining the Néron–Tate height.
without reference to a particular line bundle. (However, the height that naturally appears in the statement of the Birch–Swinnerton-Dyer conjecture is twice this height.) On abelian varieties of higher dimension, there need not be a particular choice of smallest ample line bundle to be used in defining the Néron–Tate height.
The elliptic and abelian regulators
The bilinear form associated to the canonical height 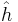 on an elliptic curve E is
on an elliptic curve E is
The elliptic regulator of E/K is
where P1,…,Pr is a basis for the Mordell-Weil group E(K) modulo torsion (cf. Gram determinant). The elliptic regulator does not depend on the choice of basis.
More generally, let A/K be an abelian variety, let B ≅ Pic0(A) be the dual abelian variety to A, and let P be the Poincaré line bundle on A × B. Then the abelian regulator of A/K is defined by choosing a basis Q1,…,Qr for the Mordell-Weil group A(K) modulo torsion and a basis η1,…,ηr for the Mordell-Weil group B(K) modulo torsion and setting
(The definitions of elliptic and abelian regulator are not entirely consistent, since if A is an elliptic curve, then the latter is 2r times the former.)
The elliptic and abelian regulators appear in the Birch–Swinnerton-Dyer conjecture.
Lower bounds for the Néron–Tate height
There are two fundamental conjectures that give lower bounds for the Néron–Tate height. In the first, the field K is fixed and the elliptic curve E/K and point P ∈ E(K) vary, while in the second, the curve E/K is fixed while the field of definition of the point P varies.
In both conjectures, the constants are positive and depend only on the indicated quantities. It is known that the abc conjecture implies Lang's conjecture.[2] The best general result on Lehmer's conjecture is the weaker estimate ![\hat h(P)\ge c(E/K)/[K(P):K]^{3%2B\epsilon}](/2012-wikipedia_en_all_nopic_01_2012/I/012b151f3693faa9a349fdbab0d9f502.png) due to Masser.[3] When the elliptic curve has complex multiplication, this has been improved to
due to Masser.[3] When the elliptic curve has complex multiplication, this has been improved to ![\hat h(P)\ge c(E/K)/[K(P):K]^{1%2B\epsilon}](/2012-wikipedia_en_all_nopic_01_2012/I/5757e742ab885e5e0a95e139f8cf3aab.png) by Laurent.[4]
by Laurent.[4]
Generalizations
A polarized algebraic dynamical system is a triple (V,φ,L) consisting of a (smooth projective) algebraic variety V, a self-morphism φ : V → V, and a line bundle L on V with the property that 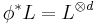 for some integer d > 1. The associated canonical height is given by the Tate limit[5]
for some integer d > 1. The associated canonical height is given by the Tate limit[5]
where φ(n) = φ o φ o … o φ is the n-fold iteration of φ. For example, any morphism φ : PN → PN of degree d > 1 yields a canonical height associated to the line bundle relation φ*O(1) = O(d). If V is defined over a number field and L is ample, then the canonical height is non-negative, and
(P is preperiodic if its forward orbit P, φ(P), φ2(P), φ3(P),… contains only finitely many distinct points.)
References
- ^ A. Néron, Quasi-fonctions et hauteurs sur les variétés abéliennes, Ann. of Math. 82 (1965), 249–331
- ^ M. Hindry and J.H. Silverman, The canonical height and integral points on elliptic curves, Invent. Math. 93 (1988), 419-450
- ^ D. Masser, Counting points of small height on elliptic curves, Bull. Soc. Math. France 117 (1989), 247-265
- ^ M. Laurent, Minoration de la hauteur de Néron-Tate, Séminaire de Théorie des Nombres (Paris 1981-1982), Progress in Mathematics, Birkhäuser 1983, 137-151
- ^ G. Call and J.H. Silverman, Canonical heights on varieties with morphisms, Compositio Math. 89 (1993), 163-205
General references for the theory of canonical heights
- E. Bombieri and W. Gubler Heights in Diophantine Geometry, ISBN 0521846153, DOI 10.2277/0521846153
- M. Hindry and J.H. Silverman, Diophantine Geometry, ISBN 0-387-98981-1
- S. Lang, Fundamentals of Diophantine Geometry, ISBN 0-387-90837-4
- J.H. Silverman, The Arithmetic of Elliptic Curves, ISBN 0-387-96203-4
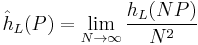
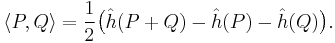
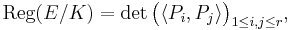
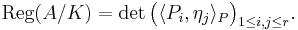
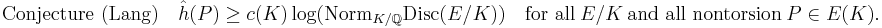
![{\rm {Conjecture}~(Lehmer)}\quad \hat h(P) \ge \frac{c(E/K)}{[K(P):K]} \quad{\rm for~all}~P\in E(\bar K).](/2012-wikipedia_en_all_nopic_01_2012/I/fb164cae04f65b5d9ce12e40ec616068.png)